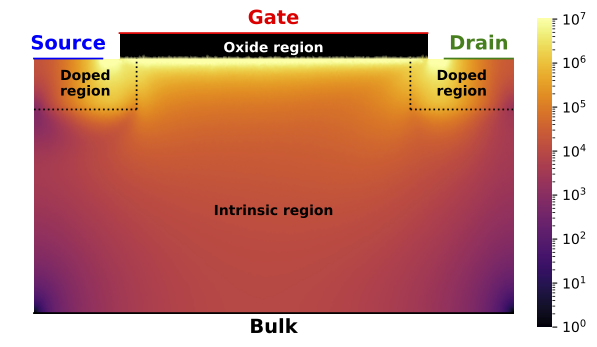
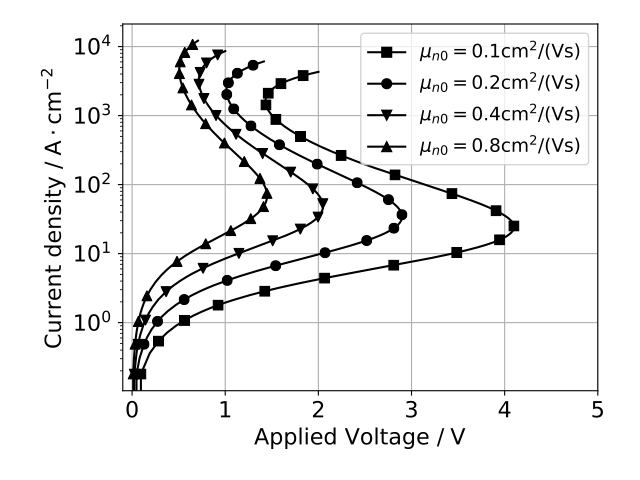
Simulated current–voltage characteristics using the electrothermal drift–diffusion model for different reference mobilities
Organic semiconductors show a complex interplay between charge-carrier and heat flow. In particular, due to Joule self-heating the temperature in an organic device increases, which in turn leads to an increase in conductivity due to temperature activated hopping transport. A positive feedback loop arises. In recent publications by our colleagues from the Dresden Integrated Center for Applied Physics and Photonic Materials (IAPP), S-shaped current-voltage characteristics of organic devices have been observed in experiments. In previous work, we have modeled this interplay via a coarse thermistor model for the net current and heat flow (see here).
In order to give a more detailed description of the processes, we extended our drift-diffusion simulation tool ddfermi to take self-heating and the positive feedback in the mobility laws, that are usually used for organic materials, into account. The details can be found in a recently published paper with out partners from the IAPP and the company m4sim GmbH in the Journal of Computational Electronics.
In the paper, an electrothermal drift–diffusion model for organic semiconductor devices with Gauss–Fermi statistics and positive temperature feedback for the charge carrier mobilities is introduced. We apply temperature-dependent Ohmic contact boundary conditions for the electrostatic potential and discretize the system by a finite volume based generalized Scharfetter–Gummel scheme. Using path-following techniques, we demonstrate that the model exhibits S-shaped current–voltage curves with regions of negative differential resistance.
Drift–diffusion simulation of S-shaped current–voltage relations for organic semiconductor devices
Duy Hai Doan, Axel Fischer, Jürgen Fuhrmann, Annegret Glitzky & Matthias Liero
Journal of Computational Electronics (2020)
https://doi.org/10.1007/s10825-020-01505-6
Open Access funding provided by Projekt DEAL. The work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—The Berlin Mathematics Research Center MATH+ (EXC-2046/1, Project ID: 390685689) in transition project SE18, Project AA2-1 and AA2-6 and the DFG Project EFOD (Grant No. RE 3198/6-1).